10800. Rectangles

There is a collection of n squares, each with a side length of 1. How many distinct rectangles can be formed using these squares?

Two rectangles are considered distinct if one cannot be rotated or moved to match the other. When constructing the rectangles, you cannot deform the squares or stack them on top of each other.

Input. One integer n (1 ≤ n ≤ 10⁹).

Output. Print the number of distinct rectangles that can be formed using the squares.

Sam[ple input	Sample output
6	8

SOLUTION

full search

Algorithm analysis

Let i * j (i ≤ j) represent the dimensions of a rectangle that can be formed using the squares. Given that i ≤ j and i * j ≤ n, it follows that i ≤ .

Let’s iterate over the smaller side of the rectangle i from 1 to . For each i, iterate over the second side j, from i until i * j ≤ n. In the variable cnt, count the number of such pairs (i, j).

cnt = 0;

for (i = 1; i <= sqrt(n); i++)

for (j = i; i * j <= n; j++)

cnt++;

The second loop can be replaced with a formula. Notice that j in the loop runs from i to n / i. Therefore, during the i-th iteration, the value of cnt increases by n / i – i + 1. The double loop can thus be rewritten as follows:

cnt = 0;

for (i = 1; i <= sqrt(n); i++)

cnt = cnt + (n / i - i + 1);

Example

Consider the first test case where n = 6. The smaller side of the rectangle iterates from 1 to = 2.

For i = 1, the second side j can take values from i = 1 to n / i = 6. This gives us 6 rectangles:

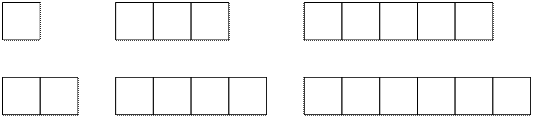
For i = 2, the second side j can take values from i = 2 to n / i = 3. This gives us 2 rectangles:

In total, for n = 6, there are 8 possible rectangles.

Algorithm realization

Read the input value of n.

scanf("%d", &n);

Compute the answer.

cnt = 0;

for (i = 1; i <= sqrt(n); i++)

cnt = cnt + (n / i – i + 1);

Print the answer.

printf("%lld\n", cnt);

Python realization

import math

Read the input value of n.

n = int(input())

Compute the answer.

cnt = 0

for i in range(1, int(math.sqrt(n)) + 1):

cnt += (n // i - i + 1)

Print the answer.

print(cnt)